dd_gauss5

Sum of five Gaussian distributions

Syntax

info = dd_gauss5()
P = dd_gauss5(r,param)
Parameters
  • r - Distance axis (N-array)
  • param - Model parameters
Returns
  • P - Distance distribution (N-array)
  • info - Model information (struct)

Model

P(r) = a_1\sqrt{\frac{2}{\pi}}\frac{1}{\sigma_1}\exp\left(-\frac{(r-\left<r_1\right>)^2}{\sigma_1^2}\right) + a_2\sqrt{\frac{2}{\pi}}\frac{1}{\sigma_2}\exp\left(-\frac{(r-\left<r_2\right>)^2}{\sigma_2^2}\right) + a_3\sqrt{\frac{2}{\pi}}\frac{1}{\sigma_3}\exp\left(-\frac{(r-\left<r_3\right>)^2}{\sigma_3^2}\right) + a_4\sqrt{\frac{2}{\pi}}\frac{1}{\sigma_4}\exp\left(-\frac{(r-\left<r_4\right>)^2}{\sigma_4^2}\right) + (1 - a_1 - a_2 - a_3 - a_4)\sqrt{\frac{2}{\pi}}\frac{1}{\sigma_5}\exp\left(-\frac{(r-\left<r_5\right>)^2}{\sigma_5^2}\right)

with \sigma_i = \mathrm{FWHM}_i/\sqrt{2ln(2)}

Variable Symbol Default Lower Upper Description
param(1) \left<r_1\right> 2.5 1.0 20 1st Gaussian center distance
param(2) \mathrm{FWHM}_1 0.5 0.2 5 1st Gaussian FWHM
param(3) a_1 0.2 0 1 1st Gaussian relative amplitude
param(4) \left<r_2\right> 3.0 1.0 20 2nd Gaussian center distance
param(5) \mathrm{FWHM}_2 0.5 0.2 5 2nd Gaussian FWHM
param(6) a_2 0.2 0 1 2nd Gaussian relative amplitude
param(7) \left<r_3\right> 3.5 1.0 20 3rd Gaussian center distance
param(8) \mathrm{FWHM}_3 0.5 0.2 5 3rd Gaussian FWHM
param(9) a_3 0.2 0 1 3rd Gaussian relative amplitude
param(10) \left<r_4\right> 4.5 1.0 20 4th Gaussian center distance
param(11) \mathrm{FWHM}_4 0.5 0.2 5 4th Gaussian FWHM
param(12) a_4 0.2 0 1 4th Gaussian relative amplitude
param(13) \left<r_5\right> 5.0 1.0 20 5th Gaussian center distance
param(14) \mathrm{FWHM}_5 0.5 0.2 5 5th Gaussian FWHM

Example using default parameters:

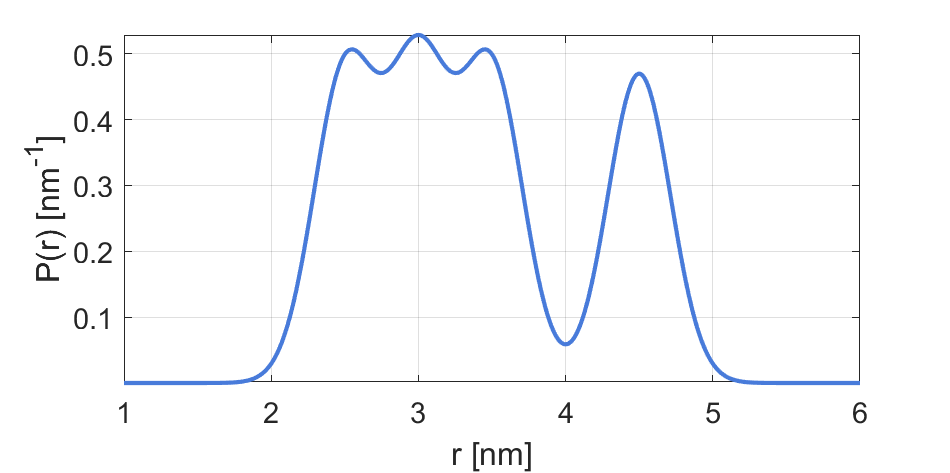
../_images/model_dd_gauss5.png

Description

info = dd_gauss5()

Returns an info structure containing the specifics of the model:

  • info.model - Full name of the parametric model.
  • info.nparam - Total number of adjustable parameters.
  • info.parameters - Structure array with information on individual parameters.
P = dd_gauss5(r,param)

Computes the distance distribution model P from the axis r according to the parameters array param. The required parameters can also be found in the info structure.