dd_shellvoidshell

Particles distributed on two spherical shells separated by a void

Syntax

info = dd_shellvoidshell()
P = dd_shellvoidshell(r,param)
Parameters
  • r - Distance axis (N-array)
  • param - Model parameters
Returns
  • P - Distance distribution (N-array)
  • info - Model information (struct)

Model

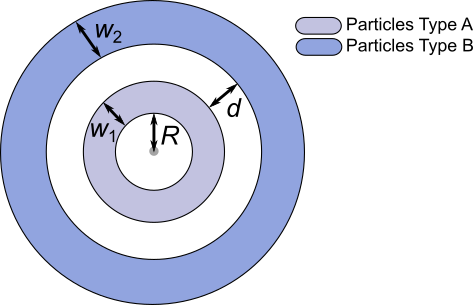
../_images/model_scheme_dd_shellvoidshell.png

P(r) = \left(R_1^3((R_3^3 - R_1^3)P_\mathrm{BS}(r|R_1,R_3) - (R_4^3 - R_1^3)P_\mathrm{BS}(r|R_1,R_4)) + R_2^3((R_4^3 - R_2^3)P_\mathrm{BS}(r|R_2,R_4) - (R_3^3 - R_2^3)P_\mathrm{BS}(r|R_2,R_3)) \right)/((R_4^3 - R_3^3)(R_2^3 - R_1^3))

with

P_\mathrm{BS}(r|R_i,R_j) = \frac{3}{16R_i^3(R_j^3 - R_i^3)}\begin{cases} 12r^3R_i^2 - r^5 \quad \text{for} \quad 0\leq r < \min(2R_i,R_j - R_i) \\ 8r^2(R_j^3 - R_i^3) - 3r(R_j^2 - R_i^2)^2 - 6r^3(R_j - R_i)(R_j + R_i) \quad \text{for} \quad R_j-R_i \leq r < 2R_i \\ 16r^2R_i^3 \quad \text{for} \quad 2R_i\leq r < R_j - R_i \\ r^5 - 6r^3(R_j^2 + R_i^2) + 8r^2(R_j^3 + R_i^3) - 3r(R_j^2 - R1_2)^2 \quad \text{for} \quad \max(R_j-R_i,2R_i) \leq r < R_i+R_j \\ 0 \quad \text{for} \quad \text{otherwise} \end{cases}

and

R_1 = R

R_2 = R + w_1

R_3 = R + w_1 + d

R_4 = R + w_1 + d + w_2

Variable Symbol Default Lower Upper Description
param(1) R 0.75 0.1 20 Sphere radius
param(2) w_1 1.00 0.1 20 1st Shell thickness
param(3) w_2 1.00 0.1 20 2nd Shell thickness
param(4) d 0.50 0.1 20 Shell-Shell separation

Example using default parameters:

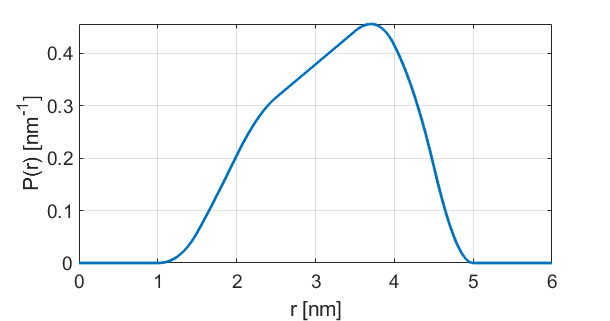
../_images/model_dd_shellvoidshell.png

Description

info = dd_shellvoidshell()

Returns an info structure containing the specifics of the model:

  • info.model - Full name of the parametric model.
  • info.nparam - Total number of adjustable parameters.
  • info.parameters - Structure array with information on individual parameters.
P = dd_shellvoidshell(r,param)

Computes the distance distribution model P from the axis r according to the parameters array param. The required parameters can also be found in the info structure.

References

[1] D.R. Kattnig, D. Hinderberger, Journal of Magnetic Resonance, 230 (2013), 50-63. DOI: 10.1016/j.jmr.2013.01.007