deerlab.bg_hom3dex_phase¶

bg_hom3dex_phase = <deerlab.model.Model object>¶

Phase shift from a homogeneous distribution of spins with excluded volume

Parameters:

tarray_like: Time vector, in microseconds.
concscalar: Spin concentration
rexscalar: Exclusion radius
lamscalar: Pathway amplitude

Returns:

Bndarray: Dipolar background vector.

Notes

Parameter Table

Name	Lower	Upper	Type	Frozen	Unit	Description
`conc`	0.01	5e+03	nonlin	No	μM	Spin concentration
`rex`	0.01	20	nonlin	No	nm	Exclusion radius
`lam`	0	1	nonlin	No		Pathway amplitude

Model

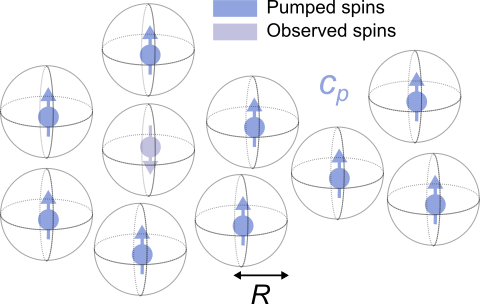
This implements the phase-shift arising from a hard-shell excluded-volume model, with spin concentration $c_s$ (in μM) and the radius of the spherical excluded volume $R_\mathrm{ex}$ (in nm).

The expression for this model is

$B(t) = \exp \Bigg(- i c_\mathrm{s}\lambda_k \bigg( V_\mathrm{ex} \mathrm{Im}\{\mathcal{K}_0(t, R_\mathrm{ex})\} + \mathcal{I}_\mathrm{C}(t) \bigg)$

where $\mathcal{I}_\mathrm{C}(t)$ is an integral without analytical form given by

$\mathcal{I}_\mathrm{C}(t) = \frac{4\pi}{3} D\,t \int_0^1 \mathrm{d}z~(1 - 3z^2) ~ \mathrm{C_i}\left( \frac{D\,t (1 - 3z^2)}{R_\mathrm{ex}^3 } \right)$

where $\mathrm{C_i}$ is the cosine integral function and $D$ is the dipolar constant

$D = \frac{\mu_0}{4\pi}\frac{(g_\mathrm{e}\mu_\mathrm{B})^2}{\hbar}$